Differenziale – was ist das? Wie das Differential der Funktion zu finden?

Zusammen mit Derivaten ihre Funktionen Differentiale – es einige der grundlegenden Konzepte der Differentialrechnung, der Hauptteil der mathematischen Analyse. Wie untrennbar miteinander verbunden sind, weit verbreitet beide von ihnen mehrere Jahrhunderte in der Lösung fast aller Probleme verwendet, die im Zuge der wissenschaftlichen und technischen Tätigkeit entstanden sind.

Die Entstehung des Begriffs des Differentials

Zum ersten Mal machte deutlich, dass ein solches Differential, einer der Gründer (zusammen mit Isaakom Nyutonom) Differentialrechnung berühmten deutschen Mathematiker Gotfrid Vilgelm Leybnits. Davor Mathematiker des 17. Jahrhunderts. sehr unklar und vage Vorstellung von etwas unendlich „ungeteilte“ von jeder bekannten Funktion, was einen sehr kleinen konstanten Wert, aber nicht gleich Null ist, unter welchen Werten die Funktion kann nicht einfach verwendet. Daher war es nur ein Schritt zur Einführung von Begriffen infinitesimal Inkrementen von Funktionsargumenten und ihre jeweiligen Schritten der Funktionen, die in Bezug auf Derivate des letzteren ausgedrückt werden kann. Und wurde dieser Schritt fast gleichzeitig die beiden oben genannten großen Wissenschaftler gemacht.

Basierend auf der Notwendigkeit, dringend praktische Mechanik Probleme, die Wissenschaft mich schnell entwickelnden Industrie und Technik konfrontiert, Newton und Leibniz geschaffen, um die gemeinsame Möglichkeiten, um die Funktionen der Änderungsrate zu finden (vor allem im Hinblick auf die mechanische Geschwindigkeit des Körpers der bekannten Trajektorie), die auf die Einführung solcher Konzepte geführt, als Ableitungsfunktion und die Differential und fand auch der Algorithmus inverse Problemlösungen wie an sich bekannt (variable) Geschwindigkeiten durchquert den Pfad zu finden, der auf dem Konzept der integralen geführt hat Ala.

In den Werken der Idee Leibniz und Newton erste schien es, dass die Differentiale – auf die Erhöhung der Grund Argumente proportional ist & Delta; h erhöht & Delta; u-Funktionen, die erfolgreich den Wert des letzteren berechnen angewendet werden kann. Mit anderen Worten, haben sie entdeckt, daß ein Inkrement Funktion an jedem Punkt sein kann (innerhalb ihres Definitionsbereiches) durch ihre Ableitung beide & Delta; u = y ‚(x) & Delta; h + αΔh wo α & Delta; h ausgedrückt wird, – Rest, auf Null, wenn & Dgr; h → neigen 0, viel schneller als die tatsächliche Ah.

Nach dem Gründer der mathematischen Analyse, die Differentiale – das ist genau das erste Glied in Schritten von allen Funktionen. Auch ohne eine klar definierte Grenzbegriff Sequenzen intuitiv verstanden werden, dass der Differenzwert der Ableitung zu funktionieren, wenn & Dgr; h neigt → 0 – & Delta; u / & Delta; h → y ‚(x).

Im Gegensatz zu Newton, der in erster Linie ein Physiker und mathematischer Apparat betrachtet als Hilfsmittel für die Untersuchung der physikalischen Probleme war, bezahlten Leibniz mehr Aufmerksamkeit auf dieses Toolkit, einschließlich einem System von visuellen und verständlichen Symbolen mathematische Werte. Er war es, die Standard-Notation der Differential Funktion dy = y '(x) dx, dx, und die Ableitung der Argumentfunktion als ihre Beziehung y' (x) = dy / dx vorgeschlagen.

Die moderne Definition

Was ist der Unterschied in Bezug auf die modernen Mathematik? Es ist eng mit dem Konzept eines variablen Inkrements zusammen. Wenn der Variable y nimmt einen ersten Wert von y y = _1, dann y = y _2, y ₂ die Differenz ─ y ₁ ist der Inkrementwert y bezeichnet. 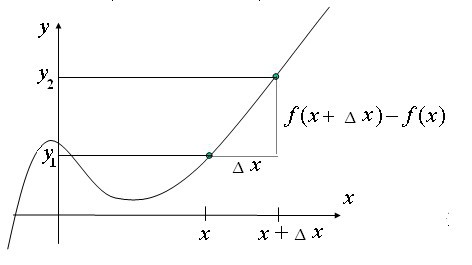Der Zuwachs kann positiv sein. negativ und Null. Das Wort „Inkrement“ bezeichnet Δ, & Delta; u Aufzeichnung (read ‚Delta-y‘) bezeichnet den Wert des Inkrement y. so & Delta; u = y ₂ y _{1 ─.}

Wenn der Wert & Delta; u beliebige Funktion y = f (x) kann als & Dgr; u = A & Delta; h + α dargestellt werden, wobei A keine Abhängigkeit von & Delta; h ist, t. E. A = const für die gegebenen x, und der Ausdruck α, wenn & Dgr; h → 0 neigt es ist sogar noch schneller als das tatsächliche & Delta; h, dann der erste ( „Master“), eine Laufzeit & Dgr; h proportional und ist für y = f (x) differential, bezeichnete Dy oder df (x) ( "y de", "de eff von X" lesen). Daher Differentiale – ein „main“ linear mit Bezug auf die Komponenten von Inkrementen & Delta; h-Funktionen.

mechanische Erklärung

Sei s = f (t) – die Entfernung in einer geraden Linie bewegenden Materialpunkt von der Anfangsposition (t – Fahrtzeit). Inkrement & Delta; s – ist der Weg Punkt während eines Zeitintervalls & Dgr; t, und die Differential ds = f ‚(t) & Delta; t – dieser Weg, der Punkt für die gleiche Zeit gehalten würde & Dgr; t, wenn sie die Geschwindigkeit f beibehalten‘ (t), zum Zeitpunkt t erreicht . Wenn ein infinitesimal & Delta; t ds unterscheidet imaginärer Weg von dem tatsächlich & Dgr; s infinitesimal eine höheren Ordnung in Bezug auf & Delta; t aufweist. Wenn die Geschwindigkeit zum Zeitpunkt t nicht gleich Null ist, gibt die ungefähren Wert ds kleinen Bias-Punkt.

geometrische Interpretation

Lassen Sie die Linie L der Graph von y = f (x) ist. Dann Δ x = MQ, & Delta; u = QM ‚(vgl. Abbildung). Tangent MN bricht & Delta; u in zwei Teile geschnitten, QN und NM‘. Erster und & Delta; h ist proportional QN = MQ ∙ tg (Winkel QMN) & Delta; h = f ‚(x), t. E QN ist dy Differential.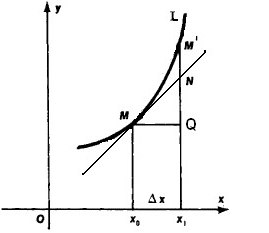

Der zweite Teil der Differenz & Delta; u NM'daet ─ dy, wenn & Delta; h → 0 NM Länge ‚verringert sich sogar schneller als der Zuwachs des Arguments, das heißt es, die Reihenfolge der Kleinheit höher als & Delta; h hat. In diesem Fall, wenn f ‚(x) ≠ 0 (nicht parallele Tangente OX) Segmente QM'i QN äquivalent; Mit anderen Worten: NM ‚schnell abnimmt (die Reihenfolge der Kleinheit seines höher) als die Gesamt Inkrement & Delta; u = QM‘. Dies zeigt sich in Figur (nähern Segment M'k M NM'sostavlyaet alle kleiner Prozentsatz QM ‚Segment).

So, differenzieller graphisch beliebige Funktion zum Inkrement der Ordinate der Tangente gleich ist.

Derivative und Differential

Ein Faktor in den ersten Term des Ausdrucks Inkrementfunktion ist auf den Wert ihrer Ableitung f ‚(x) gleich. Somit wird die folgende Beziehung – dy = f '(x) & Delta; h oder df (x) = f' (x) & Delta; h.

Es ist bekannt, dass der Zuwachs des unabhängigen Arguments seines Differential & Delta; h = dx gleich ist. Dementsprechend können wir schreiben: f ‚(x) dx = dy.

Finding Schiede zu unternehmen (manchmal die „Entscheidung“, sagte zu sein) wird durch die gleichen Regeln wie bei den Derivaten durchgeführt. Eine Liste von ihnen ist unten angegeben.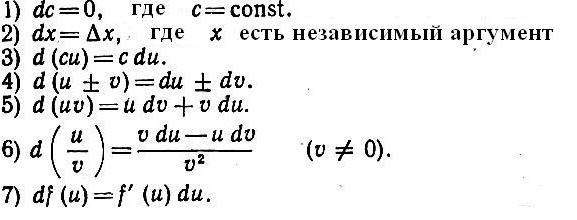

Was ist universell: die Erhöhung des Arguments oder dessen Differential

Hier ist es notwendig, einige Präzisierungen zu machen. Repräsentationswert f ‚(x) & Delta; h Differential möglich, wenn x als Argument berücksichtigen. Aber die Funktion kann ein Komplex sein, wobei x eine Funktion des Arguments t sein kann. Dann wird die Darstellung der differenziellen Expression von f ‚(x) & Delta; h, in der Regel ist es nicht möglich; außer im Fall der linearen Abhängigkeit x = at + b.

In Bezug auf die Formel f ‚(x) dx = dy, dann im Fall des unabhängigen Argument x (dann dx = & Dgr; h) im Fall der parametrischen Abhängigkeit von x t ist es Differential.

Beispielsweise ist das Ausdruck 2 x & Delta; h für y = x ² sein Differential wenn X ein Argument ist. Wir haben jetzt x = t ² und t Argument annehmen. Dann y = x ² = t ^4.

Dies wird gefolgt von (t + & Dgr; t) ² = t ² + 2tΔt + & Dgr; t ^2. Somit & Delta; h = 2tΔt + & Dgr; t ^2. Daraus folgt: 2xΔh = 2t ² (2tΔt + & Dgr; t ^2).

Dieser Ausdruck ist nicht proportional zu & Delta; t, und daher ist jetzt 2xΔh nicht differentiell. Es kann aus der Gleichung y = x ² = t ⁴ gefunden ^werden. Es ist gleich dy = 4t ³ At.

Wenn wir den Ausdruck 2xdx nehmen, ist es das Differential y = x ² für jedes Argument t. Tatsächlich , wenn x = t ² erhalten dx = 2tΔt.

So 2xdx = 2t ² 2tΔt = 4t & Dgr; t ^3, t. E. Die Expressions Differentiale aufgenommen von zwei verschiedenen Variablen übereinstimmen.

Ersetzen Schritten Differentiale

Wenn f ‚(x) ≠ 0, dann ist & Delta; u und Dy-äquivalent (wenn & Dgr; h → 0); wenn f ‚(x) = 0 (Bedeutung und dy = 0), sie sind nicht gleichwertig.

Wenn beispielsweise y = x ^2, dann & Delta; u = (x + & Delta; h) ² x ² = ─ 2xΔh + & Dgr; h ² und dy = 2xΔh. Wenn x = 3, dann haben wir & Delta; u = 6Δh + ^öh2 und dy = 6Δh , die äquivalent durch & Delta; h ist ² → 0, wenn x = 0 Wert & Delta; u = ^öh2 und dy = 0 nicht gleichwertig ist.

Diese Tatsache, zusammen mit der einfachen Struktur des Differentials (m. E. Linearität mit Bezug auf & Delta; h), wird häufig in näherungsweisen Berechnung, auf der Annahme, daß & Delta; u ≈ dy für kleines & Delta; h verwendet. Finden Sie die Differentialfunktion ist in der Regel einfacher, als den genauen Wert des Zuwachses zu berechnen.

Zum Beispiel haben wir metallischen Würfel mit Rand x = 10,00 cm. An den Rand auf & Delta; h verlängert Heizung = 0,001 cm. Wie erhöhte Volumen Würfels V? Wir haben V = x ^2, so dass dV = 3x ² = & Delta; h 3 ∙ ∙ ^{10. Februar} 0/01 = 3 (cm ^3). & Delta; V erhöht äquivalente Differenz dV, so daß & Delta; V = 3 cm ^3. Volle Berechnung würde ³ AV = 10,01 ─ ^{10. März} = 3,003001. Aber das Ergebnis aller Ziffern mit Ausnahme des ersten unzuverlässig; daher ist es immer noch notwendig , bis 3 cm ^{3 aufrunden.}

Offensichtlich ist dieser Ansatz nur sinnvoll, wenn es möglich ist, den Wert mit Fehler verliehen abzuschätzen.

Differentialfunktion: Beispiele

Lassen Sie uns versuchen , das Differential der Funktion y = x ^3, zu finden , die Ableitung zu finden. Lassen Sie uns das Argument Zuwachs & Delta; u geben und definieren.

& Delta; u = (& Delta; h + x) ³ ─ x ³ = 3x ² + & Dgr; h (& Delta; h 3xΔh ² + ^3).

Hier ist der Koeffizient A = 3x ² nicht auf & Delta; h ab, so dass der erste Term proportional & Delta; h ist, das andere Mitglied 3xΔh ^öh2 + ³ wenn & Delta; h → 0 sinkt schneller als der Zuwachs des Arguments. Folglich ist ein Mitglied der 3x ² & Delta; h die Differenz von y = x ^3:

dy = 3x ² & Delta; h = 3x ² dx oder d (x ³⁾ = 3x ² dx.

Wobei d (x ³⁾ / dx = 3x ^2.

Dy Wir finden nun die Funktion y = 1 / x durch die Ableitung. Dann d (1 / x) / dx = ─1 / x ^2. Deshalb dy = ─ & Delta; h / x ^2.

Differentiale algebraische Funktionen sind unten angegeben.

Näherungsberechnungen unter Verwendung von Differential

Um die Funktion f (x) zu bewerten und ihre Ableitung f ‚(x) bei x = a ist oft schwierig, aber das gleiche in der Nähe von x = a zu tun, ist nicht einfach. Dann kommen Sie auf die Hilfe des Näherungsausdruckes

f (a + & Delta; h) ≈ f ‚(a) & Delta; h + f (a).

Dies ergibt einen Näherungswert der Funktion zu kleinen Schritten durch die differentielle & Dgr; h f ‚(a) & Dgr; h.

Daher ergibt diese Formel einen angenäherte Ausdruck für die Funktion an dem Endpunkt eines Abschnittes einer Länge & Delta; h als Summe seines Wertes am Startpunkt des Abschnitts (x = a) und das Differentials in dem gleichen Ausgangspunkt. Genauigkeit des Verfahrens zur Bestimmung der Werte der Funktion unten zeigt die Zeichnung.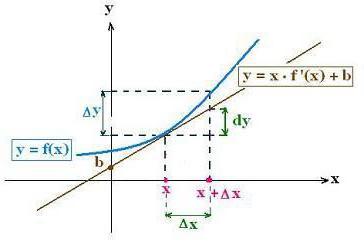

Jedoch bekannt und die genaue Ausdruck für den Wert der Funktion x = a + & Delta; h gegeben durch Formel endlicher Inkremente (oder alternativ Lagrange-Formel)

f (a + & Delta; h) ≈ f ‚(ξ) & Delta; h + f (a),

wobei der Punkt x = a + ξ im Intervall von x = a bis x = a + & Delta; h, obwohl seine genaue Position nicht bekannt ist. Die genaue Formel ermöglicht den Fehler der Näherungsformel zu bewerten. Wenn wir setzten in der Lagrange-Formel ξ = & Delta; h / 2, obwohl sie nicht mehr genau zu sein, gibt aber in der Regel eine viel bessere Lösung als der ursprüngliche Ausdruck in Bezug auf das Differential.

Auswertungsformeln Fehler durch Anwenden Differential

Meßgeräte im Prinzip ungenau, und bringen an die Messdaten zu dem Fehler entspricht. Sie werden durch limitierende gekennzeichnet die absoluten Fehler, oder, kurz gesagt, die Grenze Fehler – positive, deutlich die Fehler im Absolutwert von mehr als (oder höchstens gleich it). Die Begrenzung des relativen Fehlers wird der Quotient durch Dividieren durch den Absolutwert des gemessenen Wertes erhalten genannt.

Lassen genaue Formel y = f (x) Funktion vychislyaeniya y verwendet, aber der Wert von x ist, das Messer, und daher bringt die y-Fehler. Dann die Grenz absolute Fehler │Δu│funktsii y zu finden, die unter Verwendung der Formel

│Δu│≈│dy│ │ = f ‚(x) ││Δh│,

wo │Δh│yavlyaetsya marginal Fehlerargument. │Δu│ Menge muss nach oben gerundet werden, wie ungenaue Berechnung selbst ist der Ersatz des Zuwachses auf der Differentialrechnung.