Die Summe der Winkel eines Dreiecks. Der Satz über die Summe der Winkel eines Dreiecks

Das Dreieck ist ein Polygon mit drei Seiten (drei Winkel). Meistens bezeichnet das Teil durch Kleinbuchstaben Großbuchstaben entsprechen, die entgegengesetzte Ecken darstellen. In diesem Artikel werfen wir einen Blick auf diese Art von geometrischen Formen, Theorem, das, was die Summe der Winkel eines Dreiecks ist gleich definiert.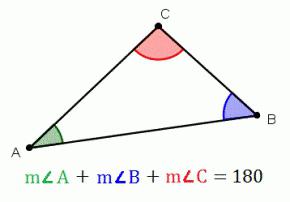

Typen größte Winkel

Die folgenden Arten von Polygon mit drei Eckpunkten:

• spitzwinkligen, bei dem alle Winkel sind scharf;
• rechteckig mit einem rechten Winkel, wobei die Seiten es, bezogen auf die Schenkel bilden, und die Seite, die entgegengesetzt zu dem rechten Winkel angeordnet ist, ist die Hypotenuse genannt;
• wenn ein stumpfer Winkel stumpf ist ;
• gleichschenklig, deren beiden Seiten gleich sind, und sie sind seitlich, und das dritte genannt – ein Dreieck mit einer Basis;
• gleichseitig mit drei gleichen Seiten.

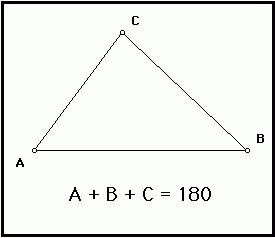
Eigenschaften

Zuzuteilen, die grundlegenden Eigenschaften, die von jeder Art von Dreieck charakteristisch sind:

• gegenüberliegende Seite der größte Winkel ist immer größer, und umgekehrt;
• kehrt sind gleiche Winkel gegenüber der gleich größten Partei und umge;
• in jedem Dreieck hat zwei spitze Winkel;
• Außenwinkel größer als jeder Innenwinkel nicht benachbart dazu;
• die Summe von zwei beliebigen Winkel stets kleiner als 180 Grad;
• Außenwinkel ist gleich der Summe der anderen beiden Ecken, die nicht mit ihm mezhuyut.

Der Satz über die Summe der Winkel eines Dreiecks

Das Theorem besagt, dass wenn man alle Ecken der geometrischen Form aufaddieren, die in der euklidischen Ebene befindet, dann ist ihre Summe 180 Grad sein. Lassen Sie uns versuchen, diesen Satz zu beweisen.

Lassen wir ein beliebiges Dreieck mit den Eckpunkten KMN haben. 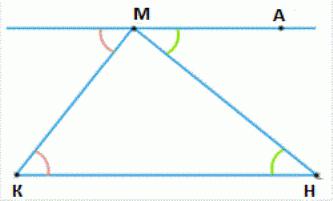Quer durch die Spitze der M hält direkt parallel zur Linie KN (selbst diese Linie namens Euklid). Es sollte angemerkt werden, Punkt A, so dass die Punkte K und A aus verschiedenen Seiten der Linie MN angeordnet sind. Wir erhalten die gleichen Winkel von AMS und MUF, die, wie das Innere, über Kreuz liegen MN zu bilden, in Verbindung mit sich kreuzenden und direkten CN MA, die parallel sind. Daraus folgt, daß die Summe der Winkel des Dreiecks, an den Scheitelpunkten M und N sich auf die Größe des CMA Winkel gleich ist. Alle drei Winkel bestehen aus einer Summe gleich der Summe der Winkel von KMA und MCS. Da die Daten an den Schnittinnenwinkel relativ seitigen parallelen Linien CL und CM MA sind, ist ihre Summe 180 Grad. Dies beweist den Satz.

Ergebnis

Von dem über dem obigen Satz impliziert die folgende logische Folge: Jedes Dreieck hat zwei spitze Winkel. Um dies zu beweisen, nehmen wir an, dass diese geometrische Figur nur einen spitzen Winkel hat. Sie können auch, dass keine der Ecken sind nicht scharf nehmen. In diesem Fall müssen sie mindestens zwei Winkel, die Größe sein, die gleich oder größer ist als 90 Grad. Aber dann ist die Summe der Winkel größer als 180 Grad. Dies kann aber nicht sein, wie nach dem Satz sum Winkel eines Dreiecks gleich 180 ° ist – nicht mehr und nicht weniger. Das ist, was hatte zu beweisen.

Eigentum Außenecken

Was ist die Summe der Winkel eines Dreiecks, die extern sind? Die Antwort auf diese Frage kann durch die Anwendung eines von zwei Arten erhalten werden. Die erste ist, dass Sie die Summe der Winkel finden müssen, die man an jedem Scheitelpunkt genommen werden, das heißt, drei Winkel. Die zweite bedeutet, dass Sie die Summe der sechs Winkel an den Ecken finden müssen. mit dem Beginn des ersten Ausführungsform zu beschäftigen. Somit enthält das Dreieck sechs äußeren Ecken – an der Spitze jeder der beiden. 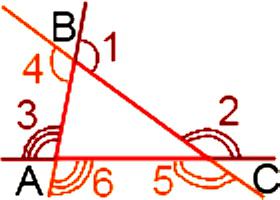Jedes Paar hat gleiche Winkel zwischen sich, da sie vertikal:

∟1 = ∟4, ∟2 = ∟5, ∟3 = ∟6.

Darüber hinaus ist bekannt, dass die äußere Ecke eines Dreiecks die Summe der beiden Innen gleich, die nicht mit ihm mezhuyutsya sind. daher

∟1 = ∟A + ∟S, ∟2 = ∟A + ∟V, ∟3 = ∟V + ∟S.

Daraus geht hervor, dass die Summe der Außenwinkel, die einer nach dem anderen in der Nähe von jedem Scheitelpunkt genommen werden, wird gleich sein:

∟1 + ∟2 + ∟3 = ∟A + + ∟S ∟A ∟V + + + ∟V ∟S = 2 x (∟A + ∟V ∟S +).

In Anbetracht der Tatsache, dass die Summe der Winkel gleich 180 Grad, kann es, dass ∟A + ∟V ∟S = + 180 ° argumentiert werden. Dies bedeutet, dass ∟1 + ∟2 + ∟3 = 2 x 180 ° = 360 °. Wenn die zweite Option verwendet wird, wird die Summe der sechs Winkel entsprechend zweimal größer. Dh die Summe der Winkel eines Dreiecks außerhalb werden sein:

∟1 + ∟2 ∟3 + + + ∟4 ∟5 + ∟6 = 2 x (∟1 + ∟2 ∟2 +) = 720 °.

rechtwinkliges Dreieck

Was ist mit der Summe der Winkel eines rechtwinkligen Dreiecks gleich ist, ist die Insel? Die Antwort ist wiederum aus Theorem, das besagt, dass die Winkel des Dreiecks auf 180 Grad addieren. Eine soliden unsere Behauptung (Eigentum) wie folgt dar: in einem rechtwinkligen Dreieck scharfer Winkel bis 90 Grad addieren. Wir beweisen seine Richtigkeit. 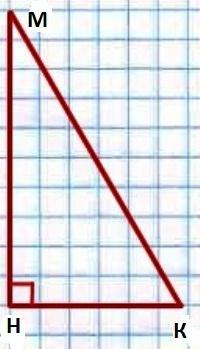Lassen Sie dort gegebenen Dreieck KMN, die ∟N = 90 °. Es ist notwendig, dass ∟K ∟M = + 90 ° zu beweisen.

So wird nach dem Satz über die Summe des Winkels ∟K + ∟M ∟N + = 180 °. In diesem Zustand wird gesagt, dass ∟N = 90 °. Es stellt sich heraus ∟K ∟M + + 90 ° = 180 °. Das ist ∟K ∟M + = 180 ° – 90 ° = 90 °. Das ist, was wir sollten beweisen.

Zusätzlich zu den oben genannten Eigenschaften eines rechtwinkligen Dreiecks, können Sie fügen Sie diese:

• Winkel, die gegen die Beine liegen, sind scharf;
• die Hypotenuse des dreieckigen größer ist als jede der Beine;
• die Summe der Beine mehr als die Hypotenuse;
• Schenkel des Dreiecks, der mit dem Winkel von 30 Grad gegenüber liegt, die Hälfte der Hypotenuse, ist, dass auf seine Hälfte gleich.

Als eine andere Eigenschaft der geometrischen Form kann Satz des Pythagoras zu unterscheiden. Sie argumentiert, dass die in einem Dreieck mit einem Winkel von 90 Grad (rechteckig), wobei die Summe der Quadrate der Beine des Quadrat der Hypotenuse entspricht.

Die Summe der Winkel eines gleichschenkligen Dreiecks

Früher haben wir gesagt, dass ein gleichschenkliges Dreieck ein Polygon mit drei Ecken ist, die zwei gleiche Seiten. Diese Eigenschaft ist bekannt geometrische Figur: die Winkel an seiner Basis gleich ist. Lassen Sie uns dies beweisen.

Nehmen Sie das Dreieck KMN, die gleichschenklig ist, SC – seine Basis. 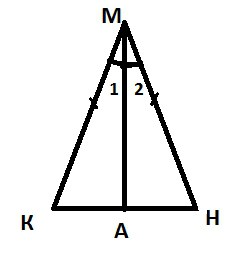Wir sind verpflichtet, dass ∟K = ∟N zu beweisen. Also, lassen Sie uns, dass die MA annehmen – KMN ist die Winkelhalbierende unseres Dreiecks. ICA Dreieck mit dem ersten Zeichen der Gleichheit Dreieck MNA. Nämlich gegeben durch Hypothese, dass die CM = NM, MA eine übliche Seite ist, ∟1 = ∟2, weil MA – diese Winkelhalbierenden. Unter Verwendung der Gleichheit der beiden Dreiecke, könnte man argumentieren, dass ∟K = ∟N. Daher ist der Satz bewiesen.

Aber wir sind interessiert an, was die Summe der Winkel eines Dreiecks (gleichschenklig). Da in dieser Hinsicht ist es nicht seine Funktionen hat, werden wir aus dem Satz zuvor diskutiert beginnen. Das heißt, können wir sagen, dass ∟K + ∟M ∟N + = 180 °, oder 2 x ∟K ∟M + = 180 ° (als ∟K = ∟N). Dadurch wird die Eigenschaft nicht beweisen, da der Satz über die Summe des Winkels eines Dreiecks wurde früher unter Beweis gestellt.

Außer den betrachteten Eigenschaften der Ecken eines Dreiecks gibt es auch so wichtige Aussagen:

• in einer gleichseitigen Dreieck Höhe, die mit der Basis abgesenkt worden war, ist gleichzeitig der Median Winkelhalbierenden des Winkels, der zwischen den gleichen Seiten ist und die Symmetrieachse seines Bodens;
• Median (Winkelhalbierende, Höhe), die an den Seiten einer geometrischen Figur gehalten werden, sind gleich.

Dreieck

Es ist auch das Recht genannt wird, ist das Dreieck, das für alle Parteien gleich sind. Und deshalb auch gleich und Winkel. Jeder von ihnen ist 60 Grad. Lassen Sie uns diese Eigenschaft unter Beweis stellen.

Nehmen wir an, dass wir ein Dreieck KMN haben. Wir wissen, dass KM = HM = KH. Dies bedeutet, dass, entsprechend die Eigenschaft des Winkels an der Basis in einem gleichseitigen Dreieck angeordnet ∟K = ∟M = ∟N. Da nach der Summe der Winkel eines Dreiecks Theorems ∟K + ∟M ∟N + = 180 ° ist, dann x 3 = 180 ° ∟K oder ∟K = 60 °, ∟M = 60 °, ∟N = 60 °. Somit ist die Behauptung bewiesen. Wie aus den obigen Erkenntnissen über den obigen Satz, wobei die Summe des Winkels basierend gesehen ein gleichseitigen Dreieck, als die Summe des Winkels von jedem anderen Dreieck ist 180 Grad. Auch in diesem Satz zu beweisen ist nicht erforderlich.

Es gibt noch einige charakteristische Eigenschaften eines gleichseitigen Dreiecks:

• Median Winkelhalbierenden Höhe in einer geometrischen Figur identisch sind, und ihre Länge wird als (A x √3) berechnet: 2;
• wenn dieser Polygon den Kreis umschreibt, dann wird der Radius (a x √3) gleich: 3;
• Wenn in einem Kreis einbeschriebenen gleichseitiges Dreieck, wäre ihr Radius (a x √3): 6;
• (A2 x √3):: Fläche der geometrischen Figur wird durch die Formel 4 berechnet.

stumpfes Dreieck

Per Definition ist ein stumpfwinkliges Dreieck, einer seiner Ecken zwischen 90 bis 180 Grad. Aber angesichts der Tatsache, dass die beiden anderen Winkel der geometrischen Form scharf, kann gefolgert werden, dass sie nicht überschreiten 90 Grad. Daher wirkt die Summe des Winkels eines Dreieck Theorem in der Summe des Winkels in einem stumpfen Dreieck zu berechnen. So können wir sicher sagen, basierend auf dem obigen Satz, daß die Summe des stumpfen Winkels eines Dreiecks ist 180 Grad. Auch dieser Satz nicht erneut Beweis benötigen.