Regelmäßiges Vieleck. Die Anzahl der Seiten eines regelmäßigen Polygons

Dreieck, Quadrat, Sechseck – diese Zahlen sind für fast jedermann bekannt. Aber auch hier, dass ein regelmäßiges Vieleck ist, weiß nicht jeder. Aber es ist alles die gleichen geometrischen Formen. Ein regelmäßiges Vieleck ist derjenige bezeichnet, der gleiche Winkel zwischen sich und der Seite hat. Diese Zahlen sind viele, aber sie alle haben die gleichen Eigenschaften, und ihnen die gleiche Formel gilt.

Eigenschaften von regelmäßig Polygonen

Alle regelmäßiges Vieleck, ob quadratisch oder Achteck, in einem Kreis eingeschrieben werden. Diese grundlegende Eigenschaft wird oft in dem Bau von Figuren verwendet. Darüber hinaus kann der Kreis in einem Polygon eingeschrieben werden, und. Die Anzahl der Kontaktstellen ist, das die Anzahl der Seiten gleich. Es ist auch wichtig, dass der Kreis in einem regelmäßigen Polygon eingeschrieben mit ihm ein gemeinsames Zentrum haben wird. Diese geometrischen Figuren unterliegen ein Theorem. Jede Partei richtig n-Ecks mit dem Radius des Kreises verbunden um es daher R. kann mit folgenden Formel berechnet werden: a = 2R ∙ sin180 °. Durch den Radius des Kreises , kann nicht nur die Parteien , sondern auch den Umfang eines Polygons gefunden werden.

Wie die Anzahl der Seiten eines regelmäßigen Polygons finden

Jede regelmäßigen n-Ecks besteht aus einer Anzahl von Segmenten gleich zueinander sind, die, wenn sie kombiniert werden , eine geschlossene Linie bilden. In diesem Fall werden alle Winkel gebildet Formen haben den gleichen Wert. Polygonen in einfache und komplexe unterteilt. Die erste Gruppe umfasst das Dreieck und Quadrat. Komplexe Polygone haben eine größere Anzahl von Seiten. Dazu gehört auch eine sternförmige Figur. In komplexen regulären Polygonseite wird durch Beschriften sie in einem Kreis gefunden. Hier ist der Beweis. Zeichnen Sie ein regelmäßiges Vieleck mit einer beliebigen Anzahl von Seiten n. Beschreiben Sie einen Kreis um ihn herum. Stellen Sie einen Radius R. Nun stell dir vor, dass einige bei n-Ecks. Wenn der Punkt seiner Ecken auf einem Kreis und gleich zueinander liegen, dann kann die Hand durch die Formel gefunden werden: a = 2R sin & alpha; ∙: 2.

Die Suche nach der Anzahl der Seiten des eingeschriebenen regelmäßigen Dreiecks

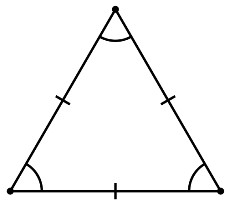
Dreieck – ist ein regelmäßiges Vieleck. Formel gilt die gleiche wie die des Quadrats angewendet werden, und die n-Ecks. Dreieck wird als gültig angesehen, wenn sie das gleiche entlang der Länge des Teils hat. Die Winkel sind gleich 60⁰. Konstrukt ein Dreieck mit Seiten vorgegebener Länge ein. Zu wissen, seine mittleren und Höhe, können Sie den Wert seiner Seiten finden. Hierzu verwenden wir ein Verfahren zur Herstellung der Formel durch eine Suche = x: cos & alpha;, wobei x – mittlere oder Höhe. Da alle Parteien gleich Dreieck sind, so erhalten wir a = b = c. Dann stimmt die folgende Aussage a = b = c = x: cos & agr;. In ähnlicher Weise können wir den Wert der Parteien in einem gleichseitigen Dreieck finden, werden aber x Höhe angegeben werden. In diesem Fall wird projiziert, streng auf der Grundlage der Zahlen sein. So, um die Höhe von x zu kennen, eine Seite eines gleichschenkligen Dreieck finden, die unter Verwendung der Formel A = B = x: cos & alpha;. Nachdem die Werte des Verbleibs von der Länge der Basis berechnet werden. Wir wenden den Satz des Pythagoras. Wir suchen eine Basishalbwerts c: 2 = √ (x: cos & agr;) ^ 2 – (x 2) = √x ^ 2 (1 – cos ^ 2α): cos 2α ^ = x ∙ tgα. Dann c = 2xtgα. Das ist die einfache Art und Weise Sie eine beliebige Anzahl von Seiten des eingeschriebenen Polygons finden.

Die Berechnung der Seiten des Platzes in einem Kreis eingeschrieben

Wie jede andere regelmäßige Polygon eingeschrieben Quadrat gleichen Seiten und Winkeln. Um es verwendet die gleiche Formel wie die eines Dreiecks. Berechnen der Seite des Platzes durch den Wert der diagonal möglich ist. Betrachten Sie diese Methode im Detail. Es ist bekannt, dass die diagonale Winkel halbiert. Anfangs war ihr Wert 90 Grad. Somit sind die beiden nach dem Dividieren des gebildeten rechtwinkligen Dreiecks. Deren Winkel an der Basis wird gleich 45 Grad sein. Dementsprechend ist jede Seite des Quadrats gleich ist, das heißt: a = b = c = d = e e√2 ∙ cos & alpha; = 2, wobei E – ist die Diagonale eines Quadrats oder eine Base nach der Teilung eines rechtwinkligen Dreiecks gebildet. Dies ist nicht der einzige Weg, um die Seiten des Platzes zu finden. Tragen Sie die Figur in einem Kreis. den Radius des Kreises R kennen, finden wir die Richtung eines Quadrats. Wir berechnen als a4 = R√2 folgt. Die Radien von regelmäßigen Polygonen werden aus der Formel berechnet , R = a: 2Tg (360 ^o: 2 n), wobei a – Seitenlänge.

Wie der Umfang des n-Ecks berechnen

Der Umfang der n-Ecks ist die Summe von allen Seiten. Es ist leicht zu berechnen. Sie müssen die Werte aller Parteien kennen. Für einige Arten von Polygonen gibt es spezielle Formeln. Sie ermöglichen es, den Umfang eines viel schneller zu finden. Es ist bekannt, dass jedes regelmäßiges Vieleck gleiche Seiten hat. Deshalb, um ihren Umfang zu berechnen, genügt es, mindestens einen von ihnen zu kennen. Die Formel wird von der Anzahl der Seiten der Form abhängen. Im Allgemeinen sieht es wie folgt aus: R = ein, in dem ein – Wertseite und n – Anzahl von Winkeln. Um zum Beispiel den Umfang eines regelmäßigen Achtecks mit einer Seitenlänge von 3 cm zu finden, müssen Sie es mit 8 multiplizieren, das heißt, P = 3 ∙ 8 = 24 cm für einen Sechseck mit einer Seitenlänge von 5 cm wird wie folgt berechnet :. P = 5 ∙ 6 = 30 cm und so für. jedes Polygon.

Das Finden des Umfangs eines Parallelogramms, quadratisch und Diamant

Je nachdem, wie viele Seiten hat ein regelmäßiges Vieleck, berechnen ihren Umfang. Dies erleichtert die Aufgabe. Tatsächlich im Gegensatz zu den anderen Stücken, in diesem Fall muss nicht für alle seine Hand zu sehen, genug von einem. Nach dem gleichen Prinzip ist am Umfang des Vierecks, das, Quadrat und Diamanten. Trotz der Tatsache, dass sie verschiedene Zahlen sind, die Formel für die man P = 4a, in dem eine – Seite. Hier ist ein Beispiel. Wenn eine Partei ein Quadrat oder eine Raute 6 cm ist, finden wir Umfang folgt: P = 4 ∙ 6 = 24 cm V Parallelogramm nur entgegengesetzte Richtungen sind .. Daher werden unter Verwendung von ihrem Umfang eine andere Methode. Also müssen wir die Länge und Breite einer Figur kennen. Dann wenden wir die Formel P = (a + b) ∙ 2. Parallelogramm, dessen Seiten alle gleich und die Winkel zwischen ihnen, genannt Diamant.

Das Finden der Umfang eines gleichseitigen Dreiecks und rechteckige

Perimeter rechts gleichseitiges Dreieck aus der Formel P = 3a zu finden, wo ein – Seitenlänge. Wenn es nicht bekannt ist, kann es durch den Median zu finden. In einem rechtwinkliges Dreieck auf den Wert sind nur zwei Seiten gleich ist. Die Basis kann durch den Satz von Pythagoras gefunden werden. Nachdem die Werte aller drei Parteien wissen, berechnen wir den Umfang. gleiche Seiten, und mit – – einem Grunde Es kann unter Verwendung der Formel R = a + b + c, wobei a und b gefunden werden. Es sei daran erinnert, dass in einem gleichseitigen Dreieck, a = b = a, dann a + b = 2a, dann P = 2a + c. Beispielsweise ist die Seite eines gleichschenkligen Dreiecks bis 4 cm gleich finden die Basis und Umfang. Berechne den Wert pythagoreischen Hypotenuse mit √ a = ² + ² = 16 = + √16 √32 = 5,65 cm. Wir berechnen nun der Umfang P = 2 ∙ 4 + 5,65 = 13,65 cm.

Wie die Winkel eines regelmäßigen Polygons finden

Ein regelmäßiges Vieleck ist in unserem Leben jeden Tag, zum Beispiel die üblichen Rechteck, Dreieck, Achteck gefunden. Es scheint, dass es nichts einfacher, als sich dieses Stück zu bauen. Aber das ist nur auf den ersten Blick. Um jeden n-Ecks zu bauen, ist es notwendig, den Wert seines Winkels zu kennen. Aber wie findet man sie? Auch alte Wissenschaftler haben versucht, regelmäßige Polygone zu bauen. Sie rechneten sie in einen Kreis zu passen. Und dann auf sie verweist auf die Notwendigkeit zu Punkt, so dass sie mit geraden Linien zu verbinden. das Problem war für den Bau von einfachen Formen gelöst. Formeln und Theoreme erhalten. Zum Beispiel kann der Euklid in seinem berühmten Werk „Home“ für Lösung von Problemen in dem 4- 3-, beteiligt, 5-, 6- und 15-Gon. Er fand Wege, um die Winkel zu bauen und zu finden. Mal sehen, wie es zu tun für die 15-Ecks. Zuerst müssen Sie die Summe seiner Innenwinkel berechnen. Es ist notwendig, mit der Formel S zu verwenden = 180⁰ (n-2). So sind wir Bei einem gegebenen 15-Ecks, also die Zahl n ist 15. Die bekannten Daten und Substituieren der Formel S = 180⁰ erhalten (15-2) = 180⁰ x 13 = 2340⁰. Wir fanden die Summe aller Innenwinkel eines 15-Ecks. Nun müssen Sie den Wert eines jeden von ihnen zu bekommen. Alle Winkel 15 machen Berechnungen 2340⁰: 15 = 156⁰. Daher ist jeder innere Winkel 156⁰, jetzt mit einem Lineal und Kompass kann die korrekte 15-Ecks konstruieren. Aber was ist komplexer n-Eck? Viele Jahrhunderte Wissenschaftler haben gekämpft, um dieses Problem zu lösen. Es wurde erst im 18. Jahrhundert von Carl Fridrihom Gaussom gefunden. Er konnte einen 65.537 Quadratmeter bauen. Seitdem wird das Problem vollständig gelöst offiziell betrachtet.

Berechnung der n-Ecks Winkel im Bogenmaß

Natürlich gibt es verschiedene Möglichkeiten, die Winkel von Polygonen zu finden. Am häufigsten werden sie in Graden berechnet. Aber wir können sie in Radiant auszudrücken. Wie kann man es machen? Gehen Sie wie folgt. Erstens haben wir die Anzahl der Seiten eines regelmäßigen Polygons herausfinden und dann subtrahieren daraus 2. Daher haben wir den Wert zu erhalten: n – 2. Multiplizieren Sie die durch die Anzahl festgestellten Differenz n ( „pi“ = 3,14). Nun teilen Sie genau das Produkt durch die Anzahl der Ecken in dem n-Ecks. Nehmen Sie das Beispiel der Daten des gleichen pyatnadtsatiugolnika berechnen. Somit ist die Zahl n gleich 15 wir die Formel S gelten = n (n – 2): n = 3,14 (15 – 2): 15 = 3,14 ∙ 13: 15 = 2,72. Dies ist natürlich nicht der einzige Weg, um den Winkel in Radianten zu berechnen. Sie können einfach die Größe eines Winkels in Grad durch die Anzahl 57.3 teilen. Immerhin ist so viel Grad zu einem Bogenmaß.

Die Berechnung der Winkel in gon

Neben Grad und Radiant Winkel eines regelmäßigen Polygons, können Sie versuchen, den Wert in Grad zu finden. Dies geschieht wie folgt. Wir subtrahieren von der Gesamtzahl 2 Winkel, durch die Anzahl der Seiten eines regelmäßigen Vielecks die resultierende Differenz dividiert wird. Gefunden das Ergebnis wird von 200. Durch die Art und Weise, diese Einheit der Messung von Winkeln, wie Gon multipliziert, kaum genutzt.

Berechnung der Außenwinkel n-gon

Alle regelmäßiges Vieleck, zusätzlich zu den inländischen, können wir berechnen, auch die äußere Ecke. Sein Wert ist die gleiche wie für die anderen Figuren. Also, einen Außenwinkel eines regelmäßigen Polygons zu finden, müssen Sie den Wert der internen wissen. Außerdem wissen wir, dass die Summe dieser beiden Winkel immer 180 Grad ist. Daher wird die Berechnung wie folgt durchgeführt: 180⁰ minus der inneren Ecke. Wir finden den Unterschied. Es wird der Wert des Winkels neben ihm sein. Zum Beispiel ist die innere Ecke des Platzes 90 Grad, dann wird das Aussehen 180⁰ sein – 90⁰ = 90⁰. Wie wir sehen können, ist es leicht zu finden. Außenwinkel kann nehmen einen Wert von + 180⁰ zu jeweils -180⁰.