Diagonal gleichseitig Trapez. Was ist die mittlere Linie des Trapezes. Arten von Trapeze. Trapeze – es ..
Trapeze – ein Sonderfall eines Vierecks, in dem ein Seitenpaar parallel ist. Der Begriff „Trapez“ stammt von dem griechischen Wort τράπεζα abgeleitet, „Tisch“, „Tabelle“ bedeutet. In diesem Artikel werden wir auf Arten von Trapez und seine Eigenschaften suchen. Außerdem betrachten wir, wie die einzelne Elemente der berechnen geometrischen Figur. Zum Beispiel kann die Diagonale eines gleichschenkligen Trapezes, die mittleren Linie, Fläche und andere. Das Material in der elementaren Geometrie populären Art enthalten, t. E. In einer leicht zugänglichen Weise.
Überblick
Lassen Sie uns zunächst verstehen, was ein Viereck. Diese Zahl ist ein Spezialfall eines Polygons mit vier Seiten und vier Ecken. Zwei Eckpunkte eines Vierecks, die nicht benachbart sind, genannt Gegenteil. Das gleiche gilt für die zwei nicht benachbarten Seiten gesagt werden. Die wichtigsten Arten von Vierecken – ein Parallelogramm, Rechteck, Raute, Quadrat, Trapez und deltoid.
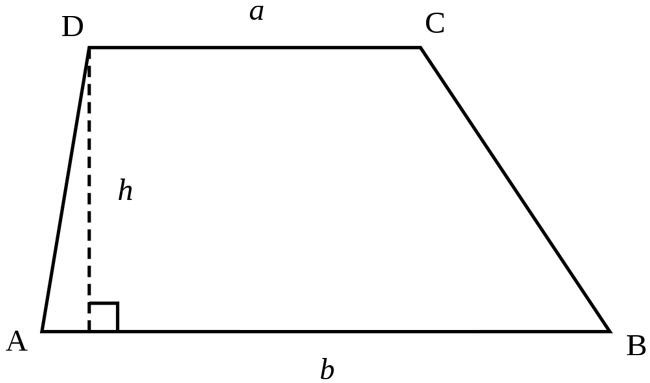
Also zurück zum Trapez. Wie wir gesagt haben, ist diese Zahl die beiden Seiten parallel. Sie sind genannt Basen. Die beiden anderen (nicht parallel) – den Seiten. Die Materialien der verschiedenen Untersuchungen und Prüfungen sehr oft können Sie Herausforderungen mit Trapeze, deren Lösung im Zusammenhang treffen sie oft den Schüler erfordert die Kenntnis vom Programm nicht abgedeckt. Schule Course Geometrie führt Schüler mit Winkeln Eigenschaften und Diagonalen sowie die Mittellinie eines gleichschenkligen Trapezes. Aber anders als das bezeichnet eine geometrische Form andere Eigenschaften hat. Aber dazu später …
Typen Trapez
Es gibt viele Arten von dieser Figur. Allerdings sind die meisten oft üblich, zwei von ihnen zu betrachten – gleichschenklig und rechteckig.
1. Rechteckige Trapezes – eine Figur, in der eine der Seiten senkrecht zur Basis. Sie hat zwei Winkel von neunzig Grad immer gleich sind.
2. gleichschenkligen Trapezes – eine geometrische Figur, dessen Seiten gleich sind. So, und die Winkel an der Basis sind auch gleich.
Die wichtigsten Grundsätze der Methoden für die Untersuchung der Eigenschaften des Trapezes
Die grundlegenden Prinzipien umfassen die Verwendung von so genannten Task-Ansatz. In der Tat gibt es keine Notwendigkeit, in einen theoretischen Kurs Geometrie der neuen Eigenschaften dieser Figur einzugeben. Sie können die verschiedenen Aufgaben der Formulierung offen oder im Prozess sein (besseres System). Es ist sehr wichtig, dass der Lehrer weiß, welche Aufgaben Sie vor Studenten zu einem bestimmten Zeitpunkt des Lernprozesses setzen müssen. Darüber hinaus kann jede trapez Eigenschaft als eine zentrale Aufgabe in dem Task-System dargestellt werden.
Das zweite Prinzip ist die so genannte Spiral Organisation der Studie „bemerkenswert“ Trapez Eigenschaften. Dies bedeutet eine Rückkehr in den Prozess auf die individuellen Merkmale der geometrischen Figur des Lernens. Somit werden die Studenten leichter, sie zu erinnern. Zum Beispiel ist die Eigenschaft der vier Punkte. Es kann wie in der Studie der Ähnlichkeit nachgewiesen werden und anschließend unter Verwendung von Vektoren. Eine gleiche Dreiecke benachbart zu den Seiten der Figur ist es möglich, durch die Verwendung nicht nur die Eigenschaften der Dreiecke mit gleichen Höhen an den Seiten, die auf einer Geraden liegen, durchgeführt, um zu beweisen, sondern auch durch die Formel S verwenden = 1/2 (AB * sin & alpha;). Darüber hinaus ist es möglich , zu erarbeiten, das Gesetz der Sinus- in die eingeschrieben oder trapez rechtwinkliges Dreieck und trapez t beschrieben. D.
Die Verwendung von „extracurricular“ verfügt über eine geometrische Figur in dem Inhalt des Schulkurses – eine ihrer Technologie Lehre Tasking. Konstante Referenz der Eigenschaften des Durchlasses des andere studieren ermöglicht es die Studierenden das Trapez tiefer zu lernen und sichert den Erfolg der Aufgabe. Also, gehen wir auf die Untersuchung dieser bemerkenswerten Figur.
Elemente und Eigenschaften eines gleichschenkligen Trapezes
Wie wir festgestellt haben, sind in dieser geometrischen Figur Seiten gleich. Doch es wird als ein Recht Trapez bekannt. Und was ist es so bemerkenswert, und warum hat seinen Namen? Die Besonderheiten dieser Figur bezieht sich, dass sie nicht nur gleich lange Seiten hat und Winkel an der Basis, sondern auch diagonal. Darüber hinaus ist die Summe der Winkel eines gleichschenkligen Trapezes auf 360 Grad gleich ist. Aber das ist nicht alles! Nur etwa gleichschenklig kann durch einen Kreis aller bekannten Trapeze beschrieben. Dies ist aufgrund der Tatsache, dass die Summe der entgegengesetzten Winkel in dieser Figur um 180 Grad ist, und nur unter dieser Bedingung kann als ein Kreis um das Viereck beschrieben. Die folgenden Eigenschaften der geometrischen Figur, sind, dass der Abstand von der Oberseite der Basis, um die Projektion der gegenüberliegenden Spitzen an der Linie, die diese Base enthält, wird zu der Mittellinie gleich sein.
Lassen Sie uns nun sehen, wie die Ecken eines gleichschenkligen Trapezes zu finden. Betrachten wir eine Lösung für dieses Problem, vorausgesetzt, dass die Größe der Figur bekannten Parteien.
Entscheidung
Es ist üblich, die Vierecke Buchstaben A, B, C, D, wo die BS und BP zu bezeichnen, – eine Grundlage. In einem gleichschenkligen Trapezoids sind Seiten gleich. Wir gehen davon aus, daß ihre Größe gleich X ist und Y Abmessungen sind Basen und Z (geringere und größere, jeweils). Für die Berechnung des Winkels der Notwendigkeit, in der Höhe H. Das Ergebnis ist ein rechtwinkliges Dreieck ABN wo AB zu verbringen – die Hypotenuse und BN und AN – die Beine. Berechnen der Größe der Bein AN: subtrahieren von der größeren Basis minimal, und das Ergebnis durch eine Formel 2. Schreiben unterteilt: (ZY) / 2 = F., nun den spitzen Winkel des Dreiecks Verwendung Funktion cos zu berechnen. Wir erhalten den folgenden Eintrag: cos (β) = X / F. Nun den Winkel berechnen: β = arcos (X / F). Weiterhin kann eine Ecke zu wissen, können wir bestimmen, und zweitens, diese elementare Rechenoperation zu machen: 180 – β. Alle Winkel definiert.
Es gibt auch eine zweite Lösung dieses Problems. Am Anfang von der Ecke in der Höhe des Beines N. berechnet den Wert der BN weggelassen. Wir wissen, dass das Quadrat der Hypotenuse eines rechtwinkligen Dreiecks auf die Summe der Quadrate der beiden anderen Seiten gleich ist. Wir erhalten: BN = √ (X2 F2). Als nächstes verwenden wir die trigonometrische Funktion tg. Das Ergebnis ist: β = arctg (BN / F). Der spitze Winkel wird gefunden. Als nächstes definieren wir einen stumpfen Winkel, wie in dem ersten Verfahren.
Die Eigenschaft der Diagonalen eines gleichschenkligen Trapezes
Zuerst schreiben wir die vier Regeln. Wenn die Diagonale in einem gleichschenkligen Trapezes senkrecht ist, dann:
– die Höhe der Figur ist gleich die Summe von Basen, dividiert durch zwei ist;
– ihre Höhe und die mittlere Linie gleich sind;
– Fläche des Trapezes ist gleich dem Quadrat der Höhe (Mittellinie auf die Hälfte Basen);
– das Quadrat der Diagonale eines Quadrats ist gleich der Hälfte der Summe des Zweifachen der quadratischen Basen oder Mittellinie (Höhe).
Jetzt sehen Sie die Formel, um die Diagonale ein gleichschenkliges Trapez definieren. Diese Information kann in vier Teile unterteilt werden:
1. Formel diagonale Länge durch die Seite.
Wir gehen davon aus, daß A – eine untere Basis, B – nach oben, C – gleichen Seiten, D – Diagonale. In diesem Fall kann die Länge bestimmt werden, wie folgt:
D = √ (C 2 + A * B).
2. Formel für die diagonale Länge des Kosinus.
Wir gehen davon aus, daß A – eine untere Basis, B – nach oben, C – gleichen Seiten, D – diagonal, α (am unteren Basis) und β (die obere Basis) – Trapezecken. Erhalten wir die folgende Formel, durch die man die Länge der Diagonale berechnen kann:
– D = √ (A2 + S2-2A * C * cos & agr;);
– D = √ (A2 + S2-2A * C * cos & beta;);
– D = √ (B2 + S2-2V * C * cos & beta;);
– D = √ (B2 + S2-2V * C * cos & agr;).
3. Formel diagonale Länge eines gleichschenkligen Trapezes.
Wir gehen davon aus, daß A – eine untere Basis, B – obere, D – diagonal, M – mittlere Linie H – Höhe, P – Bereich des Trapezoids, α und β – der Winkel zwischen Diagonalen. Bestimmen Sie die Länge der folgenden Formeln:
– D = √ (M2 + N2);
– D = √ (H 2 + (A + B) 2/4);
– D = √ (N (A + B) / sin & agr;) = √ (2n / sin & alpha;) = √ (2M * N / sin & alpha;).
Für diesen Fall der Gleichheit: sina = sin & bgr;.
4. Formel diagonale Länge durch die Seiten und die Höhe.
Wir gehen davon aus, daß A – eine untere Basis, B – nach oben, C – Seiten, D – diagonal, H – Höhe, α – Winkel mit der unteren Basis.
Bestimmen Sie die Länge der folgenden Formeln:
– D = √ (H 2 + (A-P * ctgα) 2);
– D = √ (H 2 + (B + F * ctgα) 2);
– D = √ (A2 + S2-2A * √ (C2-H 2)).
Elemente und Eigenschaften eines rechteckigen Trapezes
Schauen wir uns an, was in dieser geometrischen Figur interessiert sind. Wie wir gesagt haben, haben wir ein rechteckiges Trapez zwei rechte Winkel.
Neben der klassischen Definition gibt es andere. Zum Beispiel kann ein rechteckiges Trapez – ein Trapez, bei dem eine Seite mit der Basis senkrecht steht. Oder Form an den Seitenwinkel aufweisen. Bei dieser Art von Trapezen Höhe ist die Seite, die senkrecht zu den Basen ist. Die mittlere Linie – ein Segment, das die Mittelpunkte der beiden Seiten miteinander verbindet. Die Eigenschaft des Elements ist, dass es parallel zu den Basen und gleich der Hälfte ihrer Summe.
Nun wollen wir die grundlegenden Formeln berücksichtigen, die die geometrischen Formen definieren. Dazu nehmen wir an, dass A und B – Basis; C (senkrecht zu der Basis) und D – Seiten des rechteckigen Trapezes, M – mittlere Linie, α – spitze Winkel, P – Bereichs.
1. Die Seite senkrecht zu den Basen, eine Zahl, die gleich der Höhe (C = N), und ist gleich der Länge der zweiten Seite A und der Sinus des Winkels α in einer größeren Basis (C = A * sin & alpha;). Außerdem ist es gleich dem Produkt aus dem Tangens des spitzen Winkels α und die Differenz in der Basis: C = (A-B) * tgα.
2. Die Seiten D (nicht senkrecht zur Basis) gleich den Quotienten aus der Differenz von A und B und Cosinus (α) oder einem spitzen Winkel zu der privaten Höhe Zahlen H und sine spitzwinklig: A = (A-B) / cos α = c / sin & agr;.
3. Die Seite, die an die Basen senkrecht ist, ist gleich der Quadratwurzel des Quadrats der Differenz D – die zweite Seite – und eine quadratische Grundfläche Unterschiede:
C = √ (q2 (A-B) 2).
4. Seiten Ein rechteckiges Trapezoid ist gleich der Quadratwurzel einer Quadratsumme einer Quadratseite und C Basen geometrische Form Differenz: D = √ (C 2 + (A-B) 2).
5. Die Seite C ist gleich dem Quotienten aus dem Quadrat der doppelten Summe ihrer Basen: C = P / M = 2P / (A + B).
6. Der Bereich, der durch das Produkt M definiert ist (wobei die Mittellinie des rechteckigen Trapezes) in der Höhe oder Querrichtung senkrecht zu den Basen: P = M * N = M * C.
7. Position C ist der Quotient aus zweimal der quadratischen Form durch das Produkt sine spitze Winkel und die Summe ihrer Basen: C = P / M * sin & alpha; = 2P / ((A + B) * sin & alpha;).
8. Formel Seite eines rechteckigen Trapezes durch ihre diagonal, und der Winkel zwischen ihnen:
– sina = sin & bgr;;
– C = (D1 * D2 / (A + B)) * sin & alpha; = (D1 * D2 / (A + B)) sin & bgr; *,
wobei D1 und D2 – Diagonale des Trapezes; α und β – der Winkel zwischen ihnen.
9. Formel Seite über einen Winkel an der unteren Basis und andere: A = (A-B) / cos & alpha; = C / sin & alpha; = H / sin & agr;.
Da das Trapez mit rechtem Winkel ein Spezialfall des Trapezes ist, daß die anderen Formeln diese Zahlen bestimmen, treffen und rechteckig.
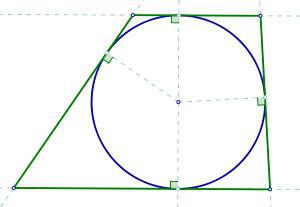
Eigenschaften incircle
Wenn die Bedingung wird gesagt, dass in einem rechtwinkligen Trapez Inkreises, dann können Sie die folgenden Eigenschaften verwenden:
– die Menge der Base ist die Summe der Seiten;
– Abstand von der Oberseite der rechteckigen Form zu den Berührungspunkten des eingeschriebenen Kreises ist immer gleich;
– Höhe des Trapezes gleich der Seite, die senkrecht zu den Basen, und ist gleich dem Durchmesser des Kreises ;
– der Kreismitte ist der Punkt , an dem sich kreuzen Bisektoren von Winkeln ;
– Wenn die laterale Seite des Kontaktstelle in Längen N und M unterteilt ist, dann ist der Radius des Kreises ist die Quadratwurzel des Produktes dieser Segmente gleich ist ;
– Viereck durch die Kontaktpunkte gebildet wird, die Oberseite des Trapezes und der Mittelpunkt des Inkreises – es ist ein Quadrat, deren Seite gleich den Radius;
– Bereich der Figur ist das Produkt des Grundes und das Produkt aus der halben Summe der Basen auf seiner Höhe.
ähnliche Trapez
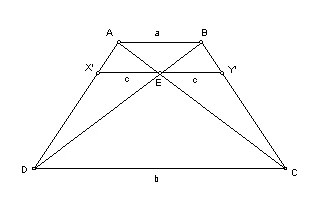
Dieses Thema ist sehr nützlich für die Eigenschaften des Studieren geometrischer Figuren. Zum Beispiel, Trapez- die diagonale Aufteilung in vier Dreiecke und sind an der Basis der gleichartigen benachbarten und zu den Seiten – der Gleich. Diese Aussage kann eine Eigenschaft der Dreiecke genannt werden, die gebrochene Trapez ist seine Diagonalen. Der erste Teil dieser Aussage wird durch das Zeichen der Ähnlichkeit der beiden Ecken bewährt. Um zu beweisen, der zweite Teil besser ist, das Verfahren unten beschrieben zu verwenden.
der Beweis
Akzeptieren Sie diese Zahl ABSD (AD und BC – die Basis des Trapezes) gebrochen ist Diagonalen HP und AC. Der Schnittpunkt – O. Wir bekommen vier Dreiecken: AOC – an der unteren Basis, BOS – die obere Basis, ABO und SOD an den Seiten. Dreiecke SOD und Biofeedback haben eine gemeinsame Höhe in diesem Fall, wenn die Segmente von BO und OD ihre Basen sind. Wir finden, dass der Unterschied ihrer Flächen (P) gleich der Differenz dieser Segmente: PBOS / PSOD = BO / ML = K. Folglich PSOD = PBOS / K. Ähnlich haben die Dreiecke AOB und Biofeedback eine gemeinsame Höhe. Akzeptiert für ihre Basissegmente SB und OA. Wir erhalten PBOS / PAOB = CO / OA = K und PAOB = PBOS / K. Daraus folgt, dass PSOD = PAOB.
Um das Material Studenten zu konsolidieren werden ermutigt, eine Verbindung zwischen den Bereichen Dreiecken finden erhalten, die gebrochene Trapez ist die Diagonalen, die nächste Aufgabe zu entscheiden. Es ist bekannt, dass Dreiecke BOS und ADP Bereiche gleich sind, ist es notwendig, die Fläche eines Trapezes zu finden. Da PSOD = PAOB, dann PABSD PBOS + = pAVK + 2 * PSOD. Aus der Ähnlichkeit der Dreiecke BOS und ANM folgt, dass BO / OD = √ (PBOS / PAOD). Folglich PBOS / PSOD = BO / OD = √ (PBOS / PAOD). Holen PSOD = √ (* PBOS pAVK). Dann PABSD PBOS + = PAOD + 2 * √ (PAOD PBOS *) = (+ √PBOS √PAOD) 2.
Eigenschaften Ähnlichkeit
Fortsetzung dieses Thema zu entwickeln, ist es möglich, und weiteres interessantes Feature der Trapeze zu beweisen. Also, mit Hilfe der Ähnlichkeit kann die Eigenschaft Segment beweisen, die den Punkt durch den Schnittpunkt der Diagonalen der geometrischen Figur gebildet durchlaufen, parallel zum Boden. Dazu lösen wir folgendes Problem: es ist notwendig, die Länge RK-Segment zu finden, die durch den Punkt O. Aus der Ähnlichkeit der Dreiecke ADP und SPU folgt, dass das AO / O = AD / BS. Aus der Ähnlichkeit der Dreiecke ADP und ASB folgt, dass AB / AC = PO / AD = BS / (BP + BS). Dies bedeutet, dass die BS * PO = AD / (AD + BC). In ähnlicher Weise aus der Ähnlichkeit der Dreiecke MLC und ABR folgt, dass OK * BP = BS / (BP + BS). Dies bedeutet, dass die OC und RC = RC = 2 * BS * AD / (AD + BC). Segment durch den Schnittpunkt der Diagonalen in zwei Hälften geteilt parallel zu der Basis und die Verbindung der beiden Seiten der Schnittpunkt passiert. Seine Länge – ist das harmonische Mittel der Vernunft Zahlen.
Betrachten Sie die folgenden Eigenschaften eines Trapezes, die die Eigenschaft haben vier Punkte genannt wird. der Schnittpunkt der Diagonalen (D), der Schnittpunkt der Fortsetzung der Seiten (E) sowie mittleren Basen (T und G) liegen immer auf der gleichen Linie. Es ist leicht, die Ähnlichkeit Methode zu beweisen. Die sich ergebenden Dreiecke sind ähnlich BES und AED, und die jeweils eine mittlere ET und DLY der Scheitelwinkel E in gleiche Teile teilen. Daher Punkt E, T und F sind kollinear. In ähnlicher Weise auf der gleichen Linie sind in Form von T angeordnet, O und G. Dies folgt aus der Ähnlichkeit der Dreiecke BOS und ANM. Daher schließen wir, dass alle vier Begriffe – E, T, O und F – auf einer geraden Linie liegen.
Unter Verwendung ähnlicher Trapezen, können die Schüler angeboten werden, um die Länge des Segments (LF) zu finden, die die Figur in zwei gleiche aufteilt. Dieser Schnitt muss an die Basen parallel sein. Da das empfangene trapez ALFD LBSF und ähnliche, die BS / LF = LF / AD. Dies bedeutet, dass LF = √ (BS * BP). Wir schließen daraus, dass das Segment, das in zwei trapez teilt dergleichen, mit einer Länge, die gleich dem geometrischen Mittel der Längen der Basen Figur hat.
Betrachten Sie die folgende Ähnlichkeitseigenschaft. An seiner Basis liegt ein Segment, das das Trapez in zwei gleich große Figuren teilt. Wir nehmen an, dass das Trapez von ABSD durch einen Abschnitt von EH in zwei ähnliche geteilt wird. Eine Höhe wird aus dem Scheitelpunkt B fallen gelassen, der durch ein Segment EH in zwei Teile – B1 und B2 geteilt wird. Wir erhalten: PABSD / 2 = (BS + EH) * B1 / 2 = (AD + EH) * B2 / 2 und PABSD = (BS + AD) * (B1 + B2) / 2. Als nächstes bilden wir ein System, dessen erste Gleichung (BS + EH) * B1 = (AD + EH) * B2 und die zweite (BS + EH) * B1 = (BS + AD) * (B1 + B2) / 2 ist. Daraus folgt, dass B2 / B1 = (BS + EH) / (AD + EH) und BS + EH = ((BS + AD) / 2) * (1 + B2 / B1). Wir erhalten, dass die Länge des Segments, das das Trapez in zwei gleiche Teile teilt, gleich der mittleren Quadratwurzellänge ist: √ ((BS2 + AD2) / 2).
Ähnlichkeitsfolgen
So haben wir das bewiesen:
1. Das Segment, das am Trapez der Mitte der lateralen Seiten verbindet, ist parallel zur Arterien und BS und ist gleich dem arithmetischen Mittel der BS und AD (die Länge der Basis des Trapezes).
2. Die Linie, die durch den Punkt O des Schnittes der Diagonalen parallel zu den AD und BS verläuft, ist gleich der mittleren Harmonischen der Ziffern AD und BS (2 * BS * AD / (BS + AD)).
3. Das Segment, das das Trapez in ähnliche teilt, hat die Länge der durchschnittlichen geometrischen Grundlagen der BS und AD.
4. Das Element, das die Figur in zwei gleiche Teile teilt, hat die Länge des mittleren Quadrats der Zahlen AD und BS.
Um das Material zu konsolidieren und die Verbindung zwischen den untersuchten Segmenten zu realisieren, muss der Student sie für ein bestimmtes Trapez bauen. Es kann leicht die Mittellinie und das Segment, das durch den Punkt O – den Schnittpunkt der Diagonalen der Figur – parallel zu den Basen verläuft, anzeigen. Aber wo wird der dritte und vierte sein? Diese Antwort führt den Schüler zur Entdeckung der gewünschten Verbindung zwischen den Mittelwerten.
Das Segment verbindet die Mittelpunkte der Diagonalen des Trapezes
Betrachten Sie die folgende Eigenschaft dieser Figur. Wir gehen davon aus, dass das Segment MN parallel zu den Basen ist und die Diagonalen halbiert. Die Kreuzungspunkte werden W und W genannt. Dieses Segment ist gleich der Basis-Halbdifferenz. Lassen Sie uns dies genauer analysieren. Die MS ist die Mittellinie des Dreiecks ABC, sie ist gleich BS / 2. MN ist die Mittellinie des Dreiecks ABD, es ist gleich AD / 2. Dann erhalten wir das M, = MN-MN und daher M, = A / 2-BC / 2 = (AD + BC) / 2.
Schwerpunkt
Schauen wir uns an, wie dieses Element für eine gegebene geometrische Figur definiert ist. Hierzu ist es notwendig, die Basen in entgegengesetzte Richtungen zu verlängern. Was bedeutet das? Es ist notwendig, die obere Unterseite die untere zu addieren – zu jeder Seite, zum Beispiel nach rechts. Und der Boden wird um die Länge der oberen linken verlängert. Dann verbinden sie mit einer Diagonale. Der Schnittpunkt dieses Segments mit der Mittellinie der Figur ist der Schwerpunkt des Trapezes.
Beschriebene und beschriebene Trapeze
Lassen Sie uns die Eigenschaften solcher Zahlen auflisten:
1. Ein Trapez kann nur dann in einen Kreis eingeschrieben werden, wenn es gleichschenklig ist.
2. Um den Umfang kann man ein Trapez beschreiben, vorausgesetzt, daß die Summe der Längen ihrer Basen gleich der Summe der Längen der Seitenwände ist.
Konsequenzen des eingeschriebenen Kreises:
1. Die Höhe des beschriebenen Trapezes ist immer gleich zwei Radien.
2. Die laterale Seite des beschriebenen Trapezes wird von der Mitte des Kreises im rechten Winkel beobachtet.
Die erste Korollar ist offensichtlich, und um die zweite zu beweisen, muss man feststellen, dass der Winkel des SOD direkt ist, was in der Tat auch nicht viel Schwierigkeiten macht. Aber die Kenntnis dieser Eigenschaft erlaubt uns, ein rechtwinkliges Dreieck bei der Lösung von Problemen anzuwenden.
Nun wollen wir diese Konsequenzen für ein gleichschenkliges Trapez konkretisieren, das in einen Kreis eingeschrieben ist. Wir bekommen, dass die Höhe das geometrische Mittel der Basis der Figur ist: H = 2R = √ (BS * AD). Ausarbeitung der grundlegenden Methode der Lösung von Problemen für Trapeze (das Prinzip der Holding zwei Höhen), muss der Schüler die folgende Aufgabe zu lösen. Wir nehmen an, dass BT die Höhe einer gleichschenkligen Figur von ABSD ist. Es ist notwendig, die Segmente AT und TD zu finden. Wenn man die oben beschriebene Formel anwendet, wird das nicht schwer zu tun sein.
Nun wollen wir herausfinden, wie man den Radius eines Kreises mit dem Bereich des beschriebenen Trapezes bestimmt. Wir senken die Höhe von der Oberseite B zur Basis des Blutdrucks. Da der Kreis in das Trapez eingeschrieben ist, dann BS + AD = 2AB oder AB = (BS + AD) / 2. Aus dem Dreieck ABN finden wir sinα = BN / AB = 2 * BN / (BS + AD). PABSD = (BS + AD) * BN / 2, BN = 2R. Wir erhalten die PABSD = (BS + AD) * R, es folgt, dass R = PABSD / (BS + AD).
. 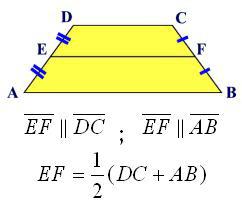
Alle Formeln der Trapez-Mittellinie
Jetzt ist es Zeit, zum letzten Element dieser geometrischen Figur zu gehen. Mal sehen, was die Mittellinie des Trapezes (M) ist:
1. Durch die Basen: M = (A + B) / 2.
2. Durch Höhe, Boden und Winkel:
• M = A-H * (ctg & alpha; + ctg & beta;) / 2;
• M = B + H * (ctg & alpha; + ctg & beta;) / 2
3. Durch die Höhe, die Diagonalen und den Winkel zwischen ihnen. Beispielsweise sind D1 und D2 Diagonalen des Trapezes; Α, β sind die Winkel zwischen ihnen:
M = D1 * D2 * sinα / 2H = D1 * D2 * sinβ / 2H.
4. Durch den Bereich und die Höhe: M = P / H.


















