Ein System linearer algebraischer Gleichungen. Homogene System von linearen algebraischen Gleichungen

In der Schule, jeder von uns untersuchte die Gleichung und, natürlich, das Gleichungssystem. Aber nicht viele Leute wissen, dass es mehr Möglichkeiten, um sich zu lösen. Heute werden wir genau sehen, alle Methoden für ein System von linearen algebraischen Gleichungen zu lösen, die aus mehr als zwei Gleichungen zusammengesetzt sind.

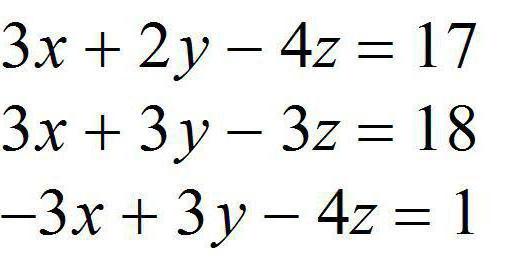
Geschichte

Heute wissen wir, dass die Kunst der Lösung von Gleichungen und ihre Systeme im alten Babylon und Ägypten entstanden. Allerdings schien Gleichheit in ihrer gewohnten Form zu uns nach dem Auftreten des Gleichheitszeichens „=“, die im Jahr 1556 vom englischen Mathematiker Rekord eingeführt wurden. Im übrigen wurde das Symbol für einen Grund gewählt: es heißt, zwei parallele gleiche Segmente. Tatsächlich ist das beste Beispiel für die Gleichstellung nicht kommen.

Der Gründer des modernen Schriftzug und Symbole nicht bekannten Umfang, der Französisch Mathematiker Fransua Viet. Allerdings ist seine Bezeichnung von heute deutlich anders. Zum Beispiel kann ein Quadrat von einer unbekannten Nummer, die er durch die Buchstaben Q (lat „quadratus“.) Bezeichnet, und den Würfel – (lat. „Cubus“) der Buchstaben C. Diese Symbole erscheinen jetzt unangenehm, aber dann war es die intuitive Art und Weise ein System von linearen algebraischen Gleichungen zu schreiben.

Allerdings war ein Nachteil bei den vorherrschenden Methoden der Lösung, dass Mathematiker nur die positiven Wurzeln betrachtet hat. Vielleicht ist dies aufgrund der Tatsache, dass negative Werte haben keine praktische Anwendung. Eine oder andere Weise, aber die erste zu betrachten negative Wurzeln begannen nach der italienischen Mathematik Niccolo Tartaglia, Gerolamo Cardano und Raphael Bombelli im 16. Jahrhundert. Eine moderne Optik, die wichtigste Methode zur Lösung quadratische Gleichungen (durch Diskriminanzanalyse) wurde im 17. Jahrhundert durch die Werke von Descartes und Newton nur etabliert.

In der Mitte des 18. Jahrhunderts Schweizer Mathematiker fand Gabriel Cramer einen neuen Weg, um die Lösung von linearen Gleichungssystemen zu erleichtern. Diese Methode wurde später nach ihm benannt, und zu diesem Tag wir sie verwenden. Aber auf der Methode der Rede Kramer etwas später, aber jetzt werden wir lineare Gleichungen diskutieren und ihre Lösungen getrennt vom System.

lineare Gleichungen

Lineare Gleichungen – die einfachste Gleichung mit Variable (n). Sie gehören zu den algebraischen. Lineare Gleichungen in der allgemeinen Form wie folgt geschrieben: a ₁ * x ₁ + a _{2 ·} x ₂ + … und _n * x _n = b. Einreichung dieses Formulars müssen wir bei der Herstellung von Systemen und Matrizen auf.

Ein System linearer algebraischer Gleichungen

Die Definition dieses Begriffs ist: eine Reihe von Gleichungen, die gemeinsame Unbekannten und die allgemeine Lösung. Typischerweise alle gelöst, in der Schule ein System mit zwei oder sogar drei Gleichungen. Aber es gibt Systeme mit vier oder mehr Komponenten. Lassen Sie uns zuerst sehen, wie man sie so aufzuschreiben, dass später war es praktisch zu lösen. Erstens sieht das System von linearen algebraischen Gleichungen besser, wenn alle Variablen wie x mit dem entsprechenden Index geschrieben werden: 1,2,3 und so weiter. Zweitens sollte es alle Gleichungen auf die kanonische Form führen: a ₁ * x ₁ + a _{2 *} x ₂ + … und _n * x _n = b.

Nach all diesen Schritten können wir damit beginnen, Ihnen zu sagen, wie die Lösung von linearen Gleichungssystemen zu finden. Sehr viel dafür wird sich als nützlich Matrix kommen.

Matrix

Matrix – eine Tabelle, die aus Zeilen und Spalten bestehen, und seine Elemente werden an ihrem Schnittpunkt. Dies kann entweder einen bestimmten Wert oder variabel sein. In den meisten Fällen, um Elemente zu bezeichnen , die unter dem tiefgestellten Indizes angeordnet sind (beispielsweise ein ₁₁ oder ₂₃ well). Der erste Index bezeichnet die Zeilennummer, und die zweite – die Spalte. Oberhalb Matrizen wie oben und jedes anderes mathematisches Element können verschiedene Operationen durchzuführen. So können Sie:

1) subtrahieren und die gleiche Größe der Tabelle hinzuzufügen.

2) Multiplizieren der Matrix auf eine beliebige Zahl oder einen Vektor.

3) Transponieren: Matrixzeilen in den Spalten zu transformieren und die Spalten – in der Schlange.

4) Multiplizieren der Matrix, wenn die Anzahl der Zeilen ist gleich einer von ihnen eine unterschiedliche Anzahl von Spalten.

im Detail all diese Techniken zu diskutieren, wie sie uns in der Zukunft nützlich sind. Subtraktion und Addition von Matrizen ist sehr einfach. Da wir die gleiche Größe Matrix nehmen, ist jedes Element aus einer Tabelle zu jedem anderen Elemente verwendet. So fügen wir (subtrahieren) zwei dieser Elemente (es ist wichtig, dass sie auf dem gleichen Boden in ihren Matrizen standen). Wenn durch die Anzahl der Matrix oder Vektor multipliziert multiplizieren man einfach jedes Element der Matrix, die durch diese Zahl (oder Vektor). Umsetzung – ein sehr interessanter Prozess. Sehr interessant ihn manchmal im realen Leben zu sehen, zum Beispiel, wenn die Ausrichtung einer Tablette oder Telefon zu ändern. Die Symbole auf dem Desktop ist eine Matrix, und mit einer Änderung der Position wird umgesetzt und breiter werden, nehmen aber in der Höhe.

Lassen Sie uns wie mehr ein Verfahren untersuchen Matrixmultiplikation. Obwohl er sagte uns, und ist nicht sinnvoll, aber bewusst sein, es immer noch nützlich ist. Multipliziere zwei Matrizen können nur unter der Bedingung, dass die Anzahl von Spalten in einer Tabelle in die Anzahl der Zeilen gleich groß ist. Nun nimmt eine Matrix Linienelemente und andere Elemente der entsprechenden Spalte. Multiplizieren , um sie miteinander und dann Summe ( das heißt, zum Beispiel, ein Produkt der Elemente ₁₁ und ₁₂ und bei ₁₂ b und ₂₂ b wird gleich: a * b _{11 12} + ₁₂ * b und _22). Somit kann ein einziges Tabellenelement, und ein Verfahren, ähnlich wie es ist weiter gefüllt.

Jetzt können wir beginnen, zu prüfen, wie Systeme von linearen Gleichungen zu lösen.

Gauss

Dieses Thema begann Ort in der Schule zu nehmen. Wir wissen sehr gut, das Konzept des „System von zwei linearen Gleichungen“ und wissen, wie sie zu lösen. Aber was, wenn die Zahl der Gleichungen größer als zwei ist? Dies wird uns helfen , Gauss – Methode.

Natürlich ist diese Methode zu verwenden, bequem, wenn Sie eine Matrix des Systems zu machen. Aber man kann es nicht konvertieren und auf eigene entscheiden.

So, wie es durch ein System von linearen Gleichungen Gauss zu lösen? By the way, obwohl diese Methode und nach ihm benannt, aber entdeckt sie in der Antike. Gauss hat eine Operation mit den Gleichungen durchgeführt, was schließlich in der Gesamtheit zu Echelon-Form zu führen. Das heißt, müssen Sie top-down (wenn es richtig platzieren) von der ersten bis zur letzten Gleichung nachgelassen eine Unbekannte. Mit anderen Worten, wir müssen dafür sorgen, dass wir haben, sagen, drei Gleichungen: die erste – drei Unbekannten, in der zweiten – zwei in der dritten – ein. Dann wird aus der letzten Gleichung, wir die ersten unbekannten finden, ersetzen seinen Wert in den zweiten oder der ersten Gleichung, und ferner die verbleibenden zwei Variablen finden.

Cramer-Regel

Für die Entwicklung dieser Technik ist es wichtig, die Fähigkeiten der Addition, Subtraktion von Matrizen sowie die Notwendigkeit, in der Lage sein zu finden Determinanten zu meistern. Deshalb, wenn Sie unbequem, dies zu tun alle sind oder nicht wissen, wie, ist es notwendig, zu lernen und trainiert werden.

Was das Wesen dieser Methode ist, und wie dies zu tun, ein System von linearen Gleichungen Cramer zu bekommen? Alles ist sehr einfach. Wir brauchen eine Matrix aus Zahlen (fast immer) die Koeffizienten eines Systems von linearen algebraischen Gleichungen zu bauen. Um dies zu tun, nehmen Sie einfach die Anzahl der Unbekannten, und wir einen Tisch in der Reihenfolge anordnen, dass sie in das System aufgenommen werden. Wenn vor der Zahl ein Zeichen „-“ ist, dann schreiben wir negative Koeffizienten. So haben wir die erste Matrix der Koeffizienten der Unbekannten, ohne die Zahl nach dem Gleichheitszeichen (natürlich, dass die Gleichung auf die kanonische Form reduziert werden muss, wenn das Recht nur eine Zahl ist, und die linke – alle Unbekannten mit Koeffizienten). Dann müssen Sie ein paar Matrizen machen – eine für jede Variable. Zu diesem Zweck wird in der ersten Matrix ist, um eine Spalte jede Spaltennummer mit den Koeffizienten nach dem Gleichheitszeichen ersetzt. So wir einige Matrizen und dann ihre Determinanten finden.

Nachdem wir die Qualifikations gefunden, es ist klein. Wir haben eine Anfangsmatrix, und es gibt mehrere Matrizen abgeleitet, die sich auf unterschiedliche Variablen entsprechen. Um eine Systemlösung zu erhalten, teilen wir die Determinante der resultierenden Tabelle auf dem bestimmenden Faktor der Tabelle. Die sich ergebende Zahl ist der Wert einer Variablen. In ähnlicher Weise finden wir die Unbekannten alle.

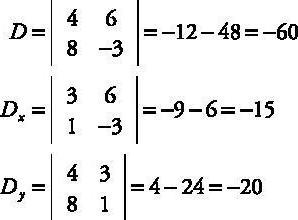
andere Methoden

Es gibt mehrere Methoden, um die Lösung von linearen Gleichungssystemen zu erhalten. Zum Beispiel kann eine sogenannte Gauss-Jordan-Verfahren, das für die Suche nach Lösungen des Systems von quadratischen Gleichungen verwendet wird, und bezieht sich auch auf die Verwendung von Matrizen. Es gibt auch ein Jacobi-Verfahren, ein System von linearen algebraischen Gleichungen zu lösen. Er passt sich an alle Computer und verwendet wird, bei der Berechnung.

komplizierte Fälle

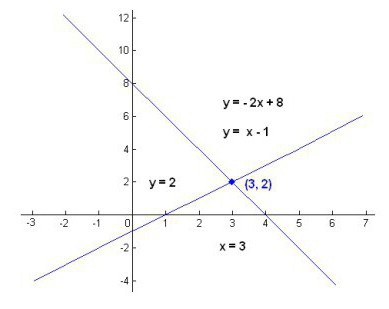
Komplexität tritt in der Regel, wenn die Anzahl der Gleichungen ist kleiner als die Anzahl von Variablen. Dann können wir mit Sicherheit sagen, dass, oder das System inkonsistent ist (dh hat keine Wurzeln), oder die Anzahl ihrer Entscheidungen gegen Unendlich. Wenn wir den zweiten Fall – ist es notwendig, die allgemeine Lösung des Systems von linearen Gleichungen zu schreiben. Es wird mindestens eine Variable enthalten.

Abschluss

Hier kommen wir zum Ende. Zusammengefasst: Wir müssen verstehen, was die Systemmatrix, erfuhr die allgemeine Lösung eines Systems von linearen Gleichungen zu finden. Darüber hinaus hielten wir andere Optionen. Wir haben herausgefunden, wie Systeme von linearen Gleichungen zu lösen: Gauß – Elimination und Cramer-Regel. Wir sprachen über schwierige Fälle und andere Möglichkeiten der Suche nach Lösungen.

In der Tat ist dieses Problem viel umfangreicher, und wenn Sie wollen besser verstehen, raten wir Sie mehr von der Fachliteratur zu lesen.